Movement of legs in gaits and otherwise are currently defined by fixed 'speed' - amount of time needed for a phase or movement to complete. Those speeds are usually set to quite low values and never anywhere near what existing servos can do.

Let's try something different now. Since we have the ability to measure current of each servo (or pair of servos, but if we move only one that would be one servo's current), we can use it to calculate a servo's speed (against manufacturer's specs) when there is no load on the servo and then store that value against calibration details to be used later.

We can use servo speeds to calculate how fast we can move legs - with a safety margin, of course.

Maths should be simple - our leg contains two servos:

• one to move thigh and
• one to move shin

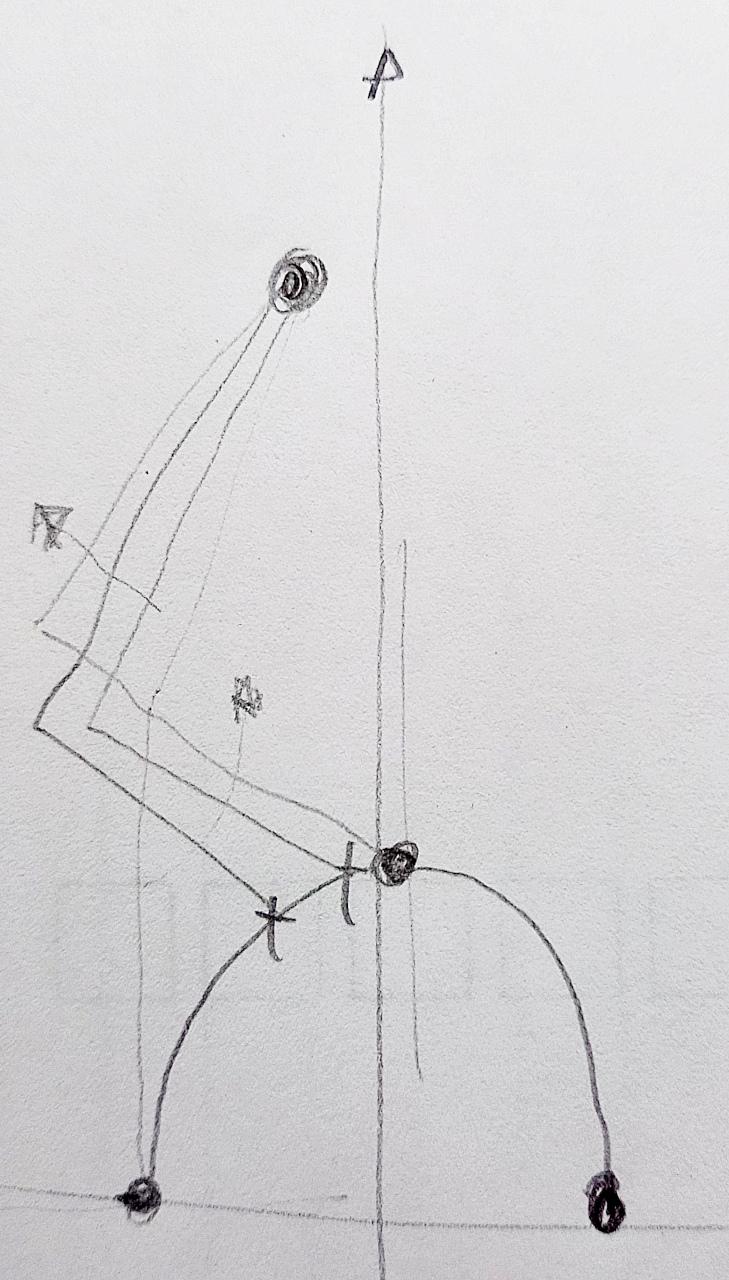If we have a path, let's say an arc when a leg is moving from the furthest back position to the front most position, and leg from a thigh servo to tip of the leg represents a circle - we can calculate where those two are intersecting given the speed of servo moving the thigh and the speed of servo moving the shin. If we calculate the speed of the thigh, we can calculate what the speed of shin would be and other way round. That's important as we would fix one and calculate another and if the result is requirement for other to move faster we can easily swap places and adjust calculation. For instance, if for given speed of servo for thigh we calculate unrealistic speed of shin servo, we can then recalculate all from maximal speed of shin servo and get slower movement of thigh servo. Easy. Right?

But, to get to servo speeds, we first need to calculate the intersection of circle (from thigh to the tip of the leg) and ellipse. For simplicity we can put an ellipse to coordinate origin and have two equations:

ellipse: x² / a² + y² / b² = 1

circle: (x - x1)² + (y - y1)² = l²

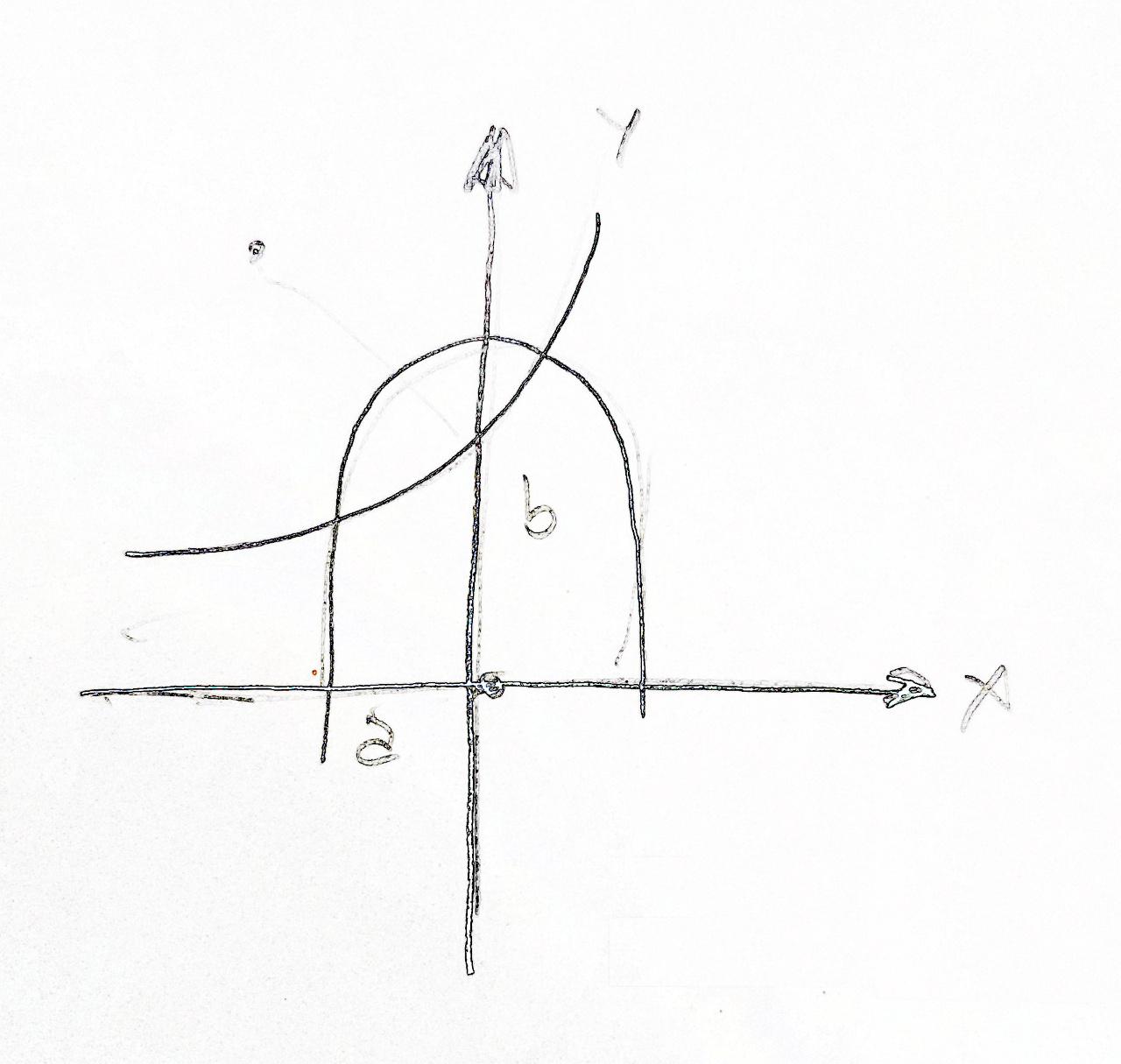
All we have to do now is to solve them.

It became quickly obvious that both equations are of second order and solution would be quadratic equation. What wasn't obvious from the beginning that it is not as trivial as it looked at the first glance!

Here it is done in neat and reputable handwriting:

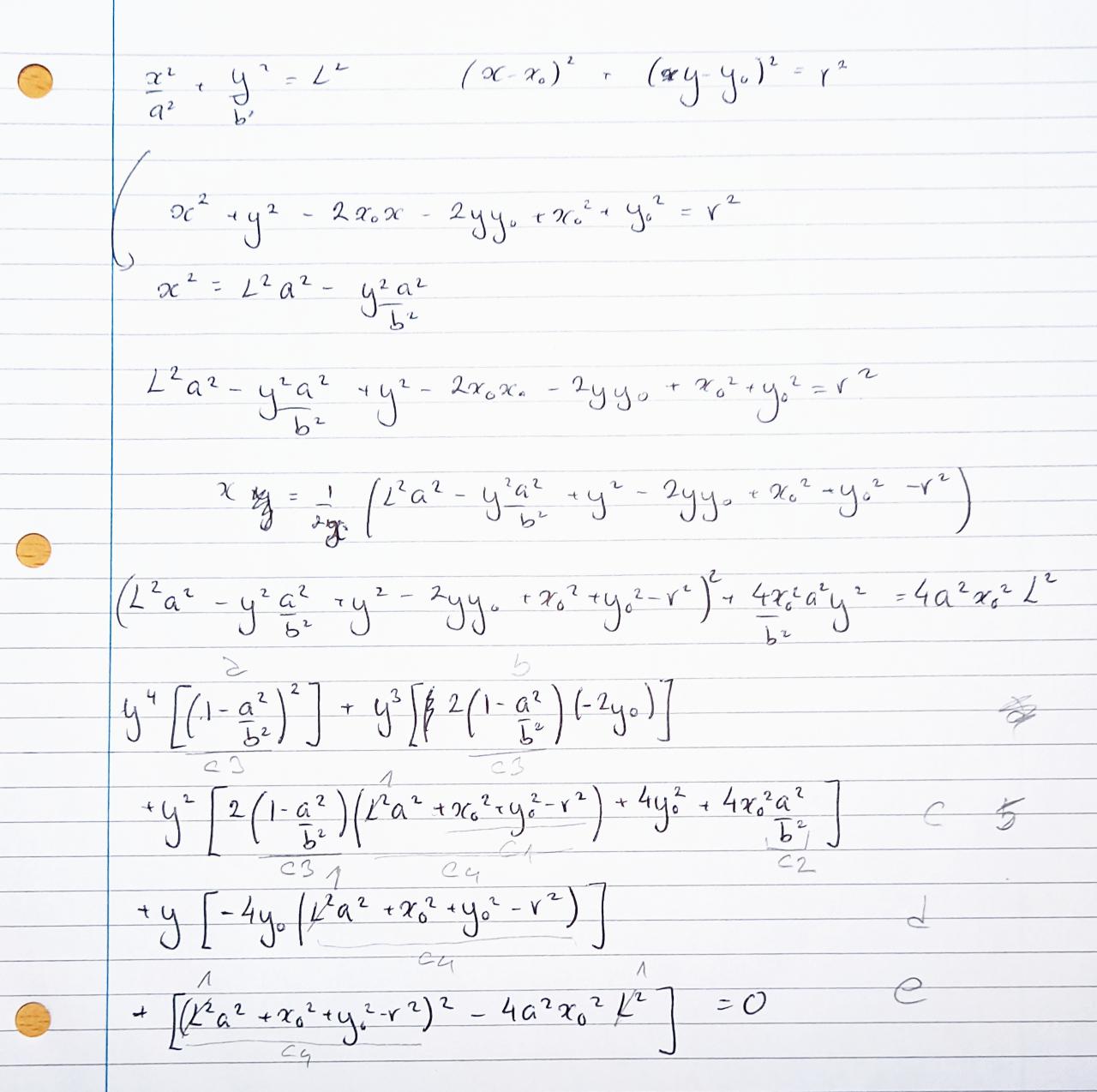
Unfortunately, transferring it to code proven too much for me at this point. Solving equation of 4th order (quartic equations) ended up in a deadend. I've used solution from Wikipedia and suggested solution by Wolfram, neatly divided all in sections, triple checked all intermediate variables, calculated and debugged discriminants - and still got impossible solutions and maths errors. Also, trying such complex, very intensive calculations (and sometimes times two when picking wrong servo speed wise), doing it for each leg and doing it at 50 times a second in Python on PiZero2W might be a bit too much. So, at this point, this line of optimisation will be mothballed for better times.

Picking constant speed is not that bad - Flig won't be able to move servos at maximal calculated and empirically determined speed for now, but doing all at much faster speed introduces some other issues which at this point in time I don't have time to deal with. So, we'll continue slow but steady!